ExP[ie xout p a1 e .
[exp|- exp[- (xout - p)/a]j (e = 0),其中1 + e (xout - p)/a > 0, -to < p < to, -to < e < to。参数p和a分别确定了位置和尺度,而形状参数e决定了FGEV(xout)的尾部行为。
GEV分布的重要性在于它是块最大值(对于k大)的极限分布。在温和条件下,几乎不考虑单个变量X(i)的常见但通常未知的分布形状,Xout(j)的分布接近GEV(图6.1)。这本质上是中心极限定理的极值模拟(Coles 2001b)。
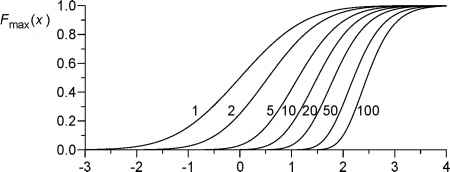
图6.1。k个独立标准正态变量最大值的分布。绘制的分布函数Fmax(x)用k标记。当k = 1时,出现标准正态分布FN(x)(公式3.49)的对称形式。一般情况下,Fmax(x) = [FN(x)]fc。让k增大有三个效果:位置(平均值)向右移动,尺度(标准差)减小,右偏度(形状参数)增加。随着k的增加,Fmax(x)趋于Fgev(x)。这是一个理论例子,有规定的FN (x)和精确确定的Fmax(x)。在实际情况下,在自变量的分布和参数未知的情况下,Fmax(x)仍然可以用Fgev(x)近似。
图6.1。k个独立标准正态变量最大值的分布。绘制的分布函数Fmax(x)用k标记。当k = 1时,出现标准正态分布FN(x)(公式3.49)的对称形式。一般情况下,Fmax(x) = [FN(x)]fc。让k增大有三个效果:位置(平均值)向右移动,尺度(标准差)减小,右偏度(形状参数)增加。随着k的增加,Fmax(x)趋于Fgev(x)。这是一个理论例子,有规定的FN (x)和精确确定的Fmax(x)。在实际情况下,在自变量的分布和参数未知的情况下,Fmax(x)仍然可以用Fgev(x)近似。
6.2.1.2极大似然估计
假设近似是完美的,块最大值{xout(j)}j'L1确实来自GEV分布(公式6.5)。进一步假设e = 0。采用最大似然原理(第2.6节,第58页)需要使似然函数(对数)最大化(Coles 2001b), ln [L(^ a,£)]= -m ln (a) -(1 + 1/£)£ln [y(j)] -£y(j), (6.6)
这篇文章有用吗?